技法|损失率_《neuralnetworkanddeeplearning》题解——ch03再看手写识别问题题解与源码分析

篇首语：本文由编程笔记#小编为大家整理，主要介绍了《neural network and deep learning》题解——ch03 再看手写识别问题题解与源码分析相关的知识，希望对你有一定的参考价值。

http://blog.csdn.net/u011239443/article/details/77649026

完整代码&＃xff1a;https://github.com/xiaoyesoso/neural-networks-and-deep-learning/blob/master/src/network2.py

我们之前根据《neural network and deep learning》题解——ch02 反向传播讲解了ch02 Network源码分析。这篇是对ch02 Network源码分析的改进。这里我们结合《机器学习技法》学习笔记12——神经网络重新讲解下。

class QuadraticCost(object):
&＃64;staticmethod
def fn(a, y):
return 0.5 * np.linalg.norm(a - y) ** 2
&＃64;staticmethod
def delta(z, a, y):
return (a - y) * sigmoid_prime(z)
class CrossEntropyCost(object):
&＃64;staticmethod
def fn(a, y):
return np.sum(np.nan_to_num(-y * np.log(a) - (1 - y) * np.log(1 - a)))
&＃64;staticmethod
def delta(z, a, y):
return (a - y)


这边我们把损失函数封装成两个类&＃xff0c;静态函数 fn 返回的是损失&＃xff0c;delta返回的是ch02 反向传播中的δ。该delta对应《机器学习技法》学习笔记12——神经网络中就是&＃xff1a;

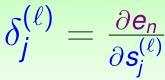
我们在Network中使用的就是二次代价函数&＃xff0c;这里我们就只讲解另外的交叉熵代价函数&＃xff1a;

对应代码&＃xff1a;

np.sum(np.nan_to_num(-y * np.log(a) - (1 - y) * np.log(1 - a)))


接下来我们来看看关于delta的问题&＃xff1a;

看看 network.py 中的 Network.cost_derivative ⽅法。这个⽅法是为⼆次代价函数写的。怎样修改可以⽤于交叉熵代价函数上&＃xff1f;你能不能想到可能在交叉熵函数上遇到的问题&＃xff1f;在 network2.py 中&＃xff0c;我们已经去掉了Network.cost_derivative ⽅法&＃xff0c;将其集成进了‘CrossEntropyCost.delta‘ ⽅法中。请问&＃xff0c;这样是如何解决你已经发现的问题的&＃xff1f;

对应《机器学习技法》学习笔记12——神经网络中&＃xff0c;cost_derivative就是




∂




e


n




∂



x


L






∂\\frace_n∂x^L


∂∂xLen​​&＃xff0c;有链式法则得到&＃xff1a;







δ


L



&＃61;




∂



e


n





∂



x


L







∂



x


L





∂



s


L







\\large δ^L &＃61; \\frac∂e_n∂x^L\\frac∂x^L∂s^L


δL&＃61;∂xL∂en​​∂sL∂xL​
network中也是的cost_derivative也是用在求δ。
而CrossEntropyCost.delta是&＃xff1a;

return (a - y)


代码 中的 a 就是上式中的x&＃xff0c;z 就是上式中的 s。
我们对CrossEntropyCost关于a求导&＃xff0c;得到&＃xff1a;






−


(



y


a



−




1


−


y




1


−


a




)


&＃61;




−


y


(


1


−


a


)


&＃43;


a


(


1


−


y


)




a


(


1


−


a


)




&＃61;




−


y


&＃43;


a




a


(


1


−


a


)






\\large -(\\fracya - \\frac1-y1-a) &＃61; \\frac-y(1-a) &＃43; a(1- y)a(1-a) &＃61; \\frac-y&＃43;aa(1-a)


−(ay​−1−a1−y​)&＃61;a(1−a)−y(1−a)&＃43;a(1−y)​&＃61;a(1−a)−y&＃43;a​
所以 CrossEntropyCost 的 cost_derivative 是






−


y


&＃43;


a




a


(


1


−


a


)





\\frac-y&＃43;aa(1-a)


a(1−a)−y&＃43;a​
由 http://blog.csdn.net/u011239443/article/details/75091283#t0 可知&＃xff1a;








∂


a




∂


z




&＃61;


a


(


1


−


a


)




\\large \\frac∂a∂z &＃61; a(1-a)


∂z∂a​&＃61;a(1−a)
所以&＃xff1a;






δ


&＃61;




∂



e


n





∂


a






∂


a




∂


z




&＃61;




−


y


&＃43;


a




a


(


1


−


a


)




a


(


1


−


a


)


&＃61;


a


−


y




\\large δ &＃61; \\frac∂e_n∂a\\frac∂a∂z &＃61; \\frac-y&＃43;aa(1-a)a(1-a) &＃61; a - y


δ&＃61;∂a∂en​​∂z∂a​&＃61;a(1−a)−y&＃43;a​a(1−a)&＃61;a−y

和Network基本上一样&＃xff0c;只不过封装成了一个default_weight_initializer函数

def __init__(self, sizes, cost&＃61;CrossEntropyCost):
self.num_layers &＃61; len(sizes)
self.sizes &＃61; sizes
self.default_weight_initializer()
self.cost &＃61; cost
def default_weight_initializer(self):
self.biases &＃61; [np.random.rand(y, 1) for y in self.sizes[1:]]
self.weights &＃61; [np.random.rand(y, x) / np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]

随机梯度下降

和Network基本上一样&＃xff0c;各个monitor是代表是否需要检测该对应的指标。

def SGD(self, training_data, epochs, mini_batch_size, eta,
lmbda&＃61;0.0,
evaluation_data&＃61;None,
monitor_evaluation_cost&＃61;False,
monitor_evaluation_accuracy&＃61;False,
monitor_training_cost&＃61;False,
monitor_training_accuray&＃61;False):
if evaluation_data:
n_data &＃61; len(evaluation_data)
n &＃61; len(training_data)
evaluation_cost, evaluation_accurary &＃61; [], []
training_cost, training_accuray &＃61; [], []
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches &＃61; [training_data[k:k &＃43; mini_batch_size] for k in range(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta, lmbda, len(training_data))
print "Epoch %s training complete" %(j&＃43;1)
if monitor_training_cost:
cost &＃61; self.total_cost(training_data, lmbda)
training_cost.append(cost)
print "Cost on train: ".format(cost)
if monitor_training_accuray:
acc &＃61; self.accuracy(training_data,covert&＃61;True)
training_accuray.append(acc)
print "Acc on train: / ".format(acc,n)
if monitor_evaluation_cost:
cost &＃61; self.total_cost(evaluation_data, lmbda,convert&＃61;True)
evaluation_cost.append(cost)
print "Cost on evaluation: ".format(cost)
if monitor_evaluation_accuracy:
acc &＃61; self.accuracy(evaluation_data)
evaluation_accurary.append(acc)
print "Acc on evaluation: / ".format(acc, n_data)
print
return evaluation_cost,evaluation_accurary,training_cost,training_accuray

反向传播

def backprop(self, x, y):
nabla_b &＃61; [np.zeros(b.shape) for b in self.biases]
nabla_w &＃61; [np.zeros(w.shape) for w in self.weights]
activation &＃61; x
activations &＃61; [x]
zs &＃61; []
for b, w in zip(self.biases, self.weights):
z &＃61; np.dot(w, activation) &＃43; b
zs.append(z)
activation &＃61; sigmoid(z)
activations.append(activation)
delta &＃61; (self.cost).delta(zs[-1], activations[-1], y)
nabla_b[-1] &＃61; delta
nabla_w[-1] &＃61; np.dot(delta, activations[-2].transpose())
for l in xrange(2, self.num_layers):
z &＃61; zs[-l]
sp &＃61; sigmoid_prime(z)
delta &＃61; np.dot(self.weights[-l &＃43; 1].transpose(), delta) * sp
nabla_b[-l] &＃61; delta
nabla_w[-l] &＃61; np.dot(delta, activations[-l - 1].transpose())
return (nabla_b, nabla_w)
def update_mini_batch(self, mini_batch, eta, lmbda, n):
nabla_b &＃61; [np.zeros(b.shape) for b in self.biases]
nabla_w &＃61; [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w &＃61; self.backprop(x, y)
nabla_b &＃61; [nb &＃43; dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w &＃61; [nw &＃43; dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights &＃61; [(1 - eta * (lmbda / n)) * w - (eta / len(mini_batch)) * nw for w, nw in
zip(self.weights, nabla_w)]
self.biases &＃61; [b - (eta / len(mini_batch)) * nb for b, nb in zip(self.biases, nabla_b)]


我们可以看到基本上和Network中一样&＃xff0c;前面已经讲解过δ。这里的代码也可以和《机器学习技法》学习笔记12——神经网络中的公式对应&＃xff1a;

L2规范化

主要区别是在最后两行更新的时候加入了L2规范化&＃xff1a;

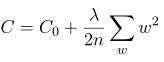
求偏导数得&＃xff1a;

则&＃xff1a;

L1规范化

这里引出了我们这节的另外一个问题&＃xff1a;

更改上⾯的代码来实现 L1 规范化

求导得到&＃xff1a;

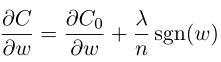
则&＃xff1a;

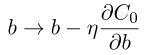
对应的代码应该写为&＃xff1a;

self.weights &＃61; [(1 - eta * (lmbda / n)*np.sign(w)) * w - (eta / len(mini_batch)) * nw for w, nw in
zip(self.weights, nabla_w) var cpro_id = "u6885494";